Hai đường thẳng vuông góc toán lớp 7 bài 2 giải bài tập
Hai đường thẳng vuông góc toán lớp 7 bài 2 giải bài tập được biên soạn từ đội ngũ giáo viên dạy giỏi môn toán trên toàn quốc đảm bảo chuẩn xác, dễ hiểu giúp các em nắm chắc tri thức trong bài hai đường thẳng vuông góc lớp 7 và hướng dẫn giải bài tập sgk về 2 đường thẳng vuông góc để các em hiểu rõ hơn.
Bài 2. Hai đường thẳng vuông góc thuộc: Chương 1: Đường thẳng vuông góc. Đường thẳng song song
I. Khái niệm hai đường thẳng vuông góc
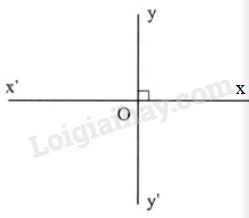
Hai đường thẳng (xx’) và (yy’) cắt nhau.
Nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu (xx’perp yy’).
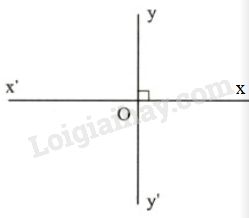
II. Vẽ hai đường thẳng vuông góc
– Ta thường dùng êke và thước thẳng để vẽ hai đường thẳng vuông góc.
– Ta thừa nhận tính chất sau:
Tính chất: Có một và chỉ một đường thẳng (a’) đi qua điểm (O) cho trước và vuông góc với đường thẳng (a) cho trước.
III. Đường trung trực của đoạn thẳng
Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng được gọi là đường trung trực của đoạn thẳng ấy.
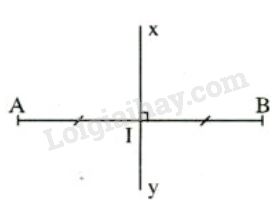
(xy) là đường trung trực của đoạn thẳng (AB.)
IV. Hướng dẫn trả lời thắc mắc sgk bài 2 hai đường thẳng vuông góc
Trả lời thắc mắc 1 Bài 2 trang 83 SGK Toán 7 Tập 1.
Đề bài: Lấy một tờ giấy gấp hai lần như hình 33. Trải phẳng tờ giấy ra rồi xem xét các nếp gấp và các góc tạo thành bởi các nếp gấp đó.
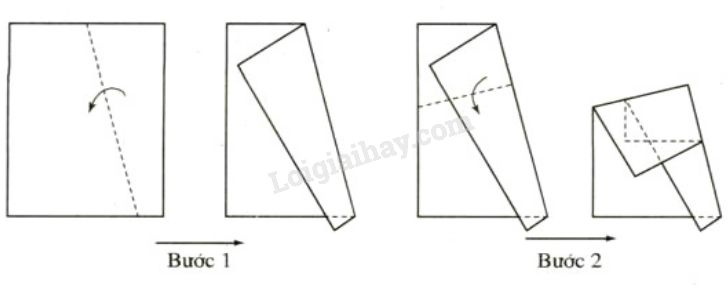
- Phương pháp giải – Xem cụ thể
Thực hành xem xét và mang ra nhận xét.
- Lời giải cụ thể
Các nếp gấp tạo thành các góc vuông.
Trả lời thắc mắc 2 Bài 2 trang 84 SGK Toán 7 Tập 1.
Đề bài: Tập suy luận
Ở hình 4, hai đường thẳng xx′ và yy′ cắt nhau tại O và góc xOy vuông. Khi đó các góc yOx′;x′Oy′;y′Ox cũng đều là những góc vuông. Vì sao ?
Hướng dẫn suy luận:
Sử dụng hai góc kề bù và hai góc đối đỉnh
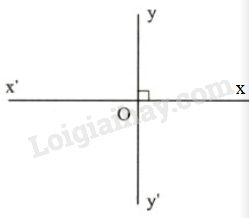
- Phương pháp giải – Xem cụ thể
Ứng dụng tính chất:
– Hai góc đối đỉnh thì bằng nhau.
– Tổng số đo hai góc kề bù bằng 180o
- Lời giải cụ thể
Ta có:
^x′Oy′ và ^xOy là hai góc đối đỉnh ⇒^x′Oy′=^xOy=90o
^xOy và ^xOy′ là hai góc kề bù ⇒^xOy+^xOy′=180o
⇒^xOy′=180o−^xOy=180o−90o=90o
^xOy′ và ^x′Oy là hai góc đối đỉnh ⇒^xOy′=^x′Oy=90o
Khi đó ^x′Oy′;^xOy′;^x′Oy đều là những góc vuông.
Trả lời thắc mắc 3 Bài 2 trang 84 SGK Toán 7 Tập 1.
Đề bài: Vẽ phác hai đường thẳng aa và a′a′ vuông góc với nhau và viết kí hiệu.
- Phương pháp giải – Xem cụ thể
Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng được gọi là đường trung trực của đoạn thẳng ấy.
- Lời giải cụ thể
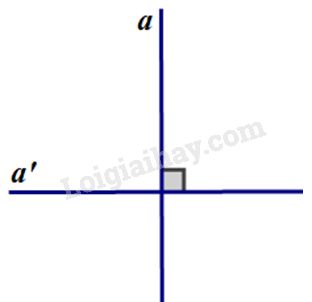
Kí hiệu: a⊥a′a⊥a′
Trả lời thắc mắc 4 Bài 2 trang 84 SGK Toán 7 Tập 1.
Đề bài: Cho một điểm OO và một đường thẳng a.a. Hãy vẽ đường thẳng a′a′ đi qua OO và vuông góc với đường thẳng a.a.
- Phương pháp giải – Xem cụ thể
Sử dụng thước thẳng và êke để vẽ hình.
- Lời giải cụ thể
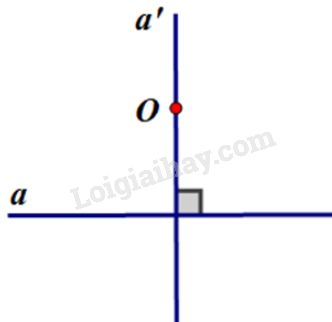
V. Hướng dẫn giải bài tập về hai đường vuông góc
Bài 11 trang 86 SGK Toán 7 tập 1.
Đề bài: Điền vào chỗ trống (…) trong các phát biểu sau:
a) Hai đường thẳng vuông góc với nhau là hai đường thẳng …
b) Hai đường thẳng aa và a′a′ vuông góc với nhau được ký hiệu là …
c) Cho trước một điểm AA và đường thẳng dd …đường thẳng d′d′ đi qua AA và vuông góc với dd.
- Phương pháp giải – Xem cụ thể
– Khái niệm: Hai đường thẳng xx′xx′ và yy′yy′ cắt nhau. Nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu xx′⊥yy′xx′⊥yy′.
– Tính chất: Có một và chỉ một đường thẳng a′a′ đi qua điểm OO cho trước và vuông góc với đường thẳng aa cho trước.
- Lời giải cụ thể
a) Hai đường thẳng vuông góc với nhau là hai đường thẳng cắt nhau tạo thành một góc vuông.
b) Hai đường thẳng aa và a′a′ vuông góc với nhau được kí hiệu là a⊥a′a⊥a′.
c) Cho trước một điểm AA và đường thẳng dd. Có một và chỉ một đường thẳng d′d′ đi qua AA và vuông góc với dd.
Bài 12 trang 86 SGK Toán 7 tập 1.
Đề bài: Trong hai câu sau, câu nào đúng? câu nào sai? Hãy bác bỏ câu sai bằng một hình vẽ.
a) Hai đường thẳng vuông góc thì cắt nhau.
b) Hai đường thẳng cắt nhau thì vuông góc.
- Phương pháp giải – Xem cụ thể
Hai đường thẳng xx′ và yy′ cắt nhau. Nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu xx′⊥yy′.
- Lời giải cụ thể
a) Đúng (theo khái niệm).
b) Sai. Ví dụ hình vẽ sau hai đường thẳng a và b cắt nhau tại O nhưng a không vuông góc với b.
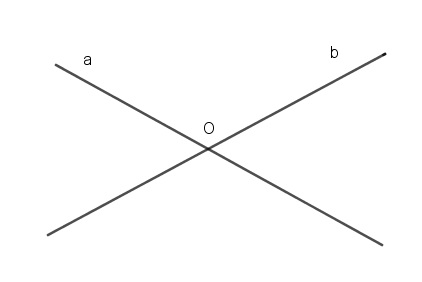
Bài 13 trang 86 SGK Toán 7 tập 1.
Đề bài: Vẽ một đoạn thẳng ABAB trên giấy trong hoặc giấy mỏng. Hãy gấp tờ giấy để nếp gấp trùng với đường trung trực của đoạn thẳng ấy.
- Phương pháp giải – Xem cụ thể
+ Vẽ đoạn thẳng ABAB trên giấy.
+ Gấp giấy theo hướng dẫn.
+ Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy
- Lời giải cụ thể
Gấp tờ giấy sao cho điểm AA trùng với điểm B.B. Khi đó nếp gấp sẽ trùng với đường trung trực của đoạn thẳng ABAB.
Bài 14 trang 86 SGK Toán 7 tập 1.
Đề bài: Cho đoạn thẳng CDCD dài 3cm.3cm. Hãy vẽ đường trung trực của đoạn thẳng ấy.
- Phương pháp giải – Xem cụ thể
+ Vẽ đoạn thẳng CDCD dài 3cm.3cm.
+ Lấy II là trung điểm của CD.CD.
+ Vẽ đường trung trực của đoạn thẳng CD.CD.
- Lời giải cụ thể
– Phương pháp vẽ:
– Dùng thước có chia khoảng, vẽ đoạn thẳng CD=3cmCD=3cm. Vẽ trung điểm II của CDCD bằng cách lấy II sao cho CI=1,5cm.CI=1,5cm.
– Dùng êke vẽ đường thẳng dd vuông góc với CDCD tại II.
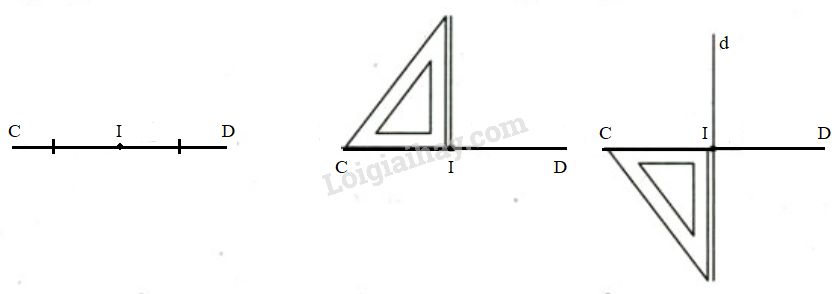
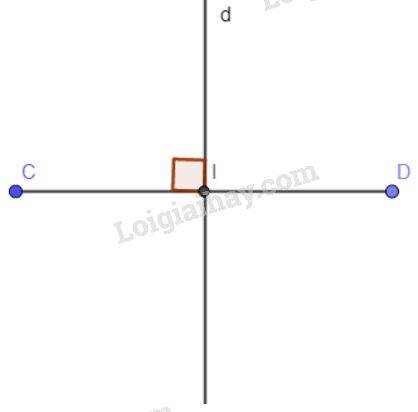
Đường thẳng dd chính là đường trung trực của đoạn thẳng CD.CD.
Bài 15 trang 86 SGK Toán 7 tập 1.
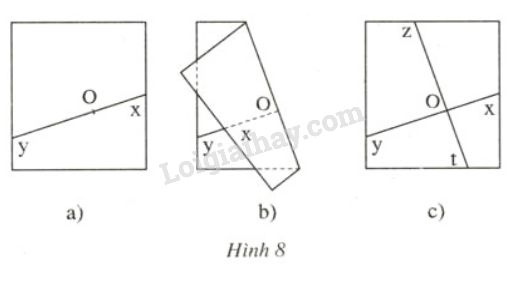
Đề bài: Vẽ đường thẳng xyxy và điểm OO thuộc đường thẳng đó trên giấy trong (như hình 8a). Gấp giấy như hình 8b. Trải phẳng tờ giấy rồi tô xanh nếp gấp ztzt (hình 8c). Hãy nêu những tổng kết rút ra từ các hoạt động trên.
- Phương pháp giải – Xem cụ thể
Xem xét hình và mang ra nhận xét.
- Lời giải cụ thể
Tổng kết rút ra từ các hoạt động trên: Nếp gấp ztzt vuông góc với đường thẳng xyxy tại O.O. Có bốn góc vuông là ˆxOz,ˆyOz,ˆyOt,ˆtOx.
Bài 16 trang 87 SGK Toán 7 tập 1.
Đề bài: Vẽ đường thẳng d′ đi qua điểm A và vuông góc với đường thẳng d cho trước chỉ bằng êke.
- Phương pháp giải – Xem cụ thể
Hai đường thẳng xx′ và yy′ cắt nhau.
Nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu xx′⊥yy′.
- Lời giải cụ thể
Thứ tự vẽ đường thẳng d′ và d′⊥d như sau:
– Vẽ đường thẳng d, lấy điểm A nằm ngoài đường thẳng d.
– Đặt êke sao cho một mép góc vuông của êke đi qua điểm A, mép góc vuông kia của êke nằm trên đường thẳng d.
– Kẻ đoạn thẳng theo mép góc vuông của êke đi qua điểm A.
– Dùng êke kéo dài đoạn thẳng trên về hai phía thành đường thẳng d′ vuông góc với d.
Xem hình vẽ sau đây:
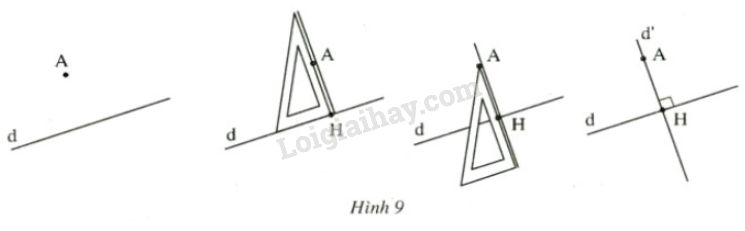
Bài 17 trang 87 SGK Toán 7 tập 1.
Đề bài: Dùng êke hãy xác minh xem hai đường thẳng aa và a′a′ ở hình vẽ (a, b, c) có vuông góc với nhau hay không?
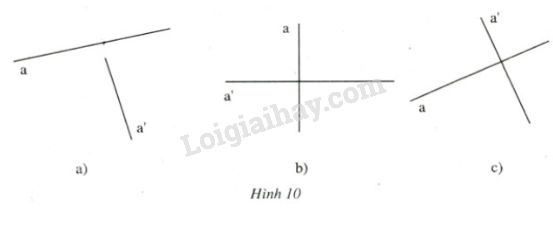
- Phương pháp giải – Xem cụ thể
Dùng êke để xác minh rồi nhận xét.
- Lời giải cụ thể
Dùng êke xác minh ta được:
a) aa không vuông góc với a′a′;
b) a⊥a′a⊥a′;
c) a⊥a′a⊥a′.
Bài 18 trang 87 SGK Toán 7 tập 1.
Đề bài:Vẽ hình theo cách diễn tả bằng lời sau:
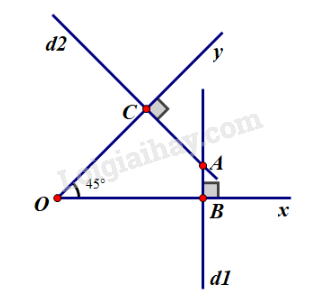
Vẽ góc xOyxOy có số đo bằng 45∘45∘. Lấy điểm AA bất kì nằm trong góc xOy.xOy. Vẽ qua AA đường thẳng d1d1 vuông góc với tia OxOx tại B.B. Vẽ qua AA đường thẳng d2d2 vuông góc với tia OyOy tại C.C.
- Phương pháp giải – Xem cụ thể
Thực hiện vẽ hình lần lượt theo các bước yêu cầu của bài toán.
- Lời giải cụ thể
Sau khoảng thời gian vẽ ta được hình sau đây:
Bài 19 trang 87 SGK Toán 7 tập 1.
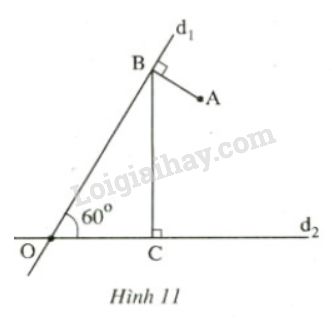
Đề bài: Vẽ lại hình bên và nói rõ trình tự vẽ hình.
Lưu ý: Có thể vẽ hình theo nhiều trình tự khác nhau.
- Phương pháp giải – Xem cụ thể
Cách dựng góc biết số đo, đường vuông góc .
- Lời giải cụ thể
Có thể vẽ hình đã cho theo nhiều trình tự khác nhau.
Ví dụ:
Trình tự 1:
– Vẽ đường thẳng d2d2 bất kì.
– Vẽ đường thẳng d1d1 cắt d2d2 tại OO và tạo ˆd1Od2=60∘d1Od2^=60∘.
– Vẽ điểm AA tùy ý nằm trong ˆd1Od2d1Od2^.
– Vẽ đoạn thẳng ABAB vuông góc d1d1 tại B.B.
– Vẽ đoạn thẳng BCBC vuông góc với d2d2 tại C.C.
Trình tự 2:
– Vẽ hai đường thẳng d1,d2d1,d2 cắt nhau tại OO và tạo ˆd1Od2=60∘d1Od2^=60∘.
– Lấy điểm BB tùy ý nằm trên tia Od1Od1.
– Vẽ đoạn thẳng BCBC vuông góc với tia Od2Od2 tại CC, điểm CC nằm trên tia Od2Od2.
– Vẽ đoạn thẳng BABA vuông góc với tia Od1Od1 tại BB, điểm AA nằm trong góc ˆd1Od2d1Od2^.
Bài 20 trang 87 SGK Toán 7 tập 1.
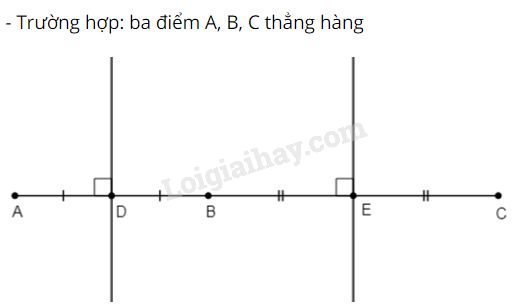
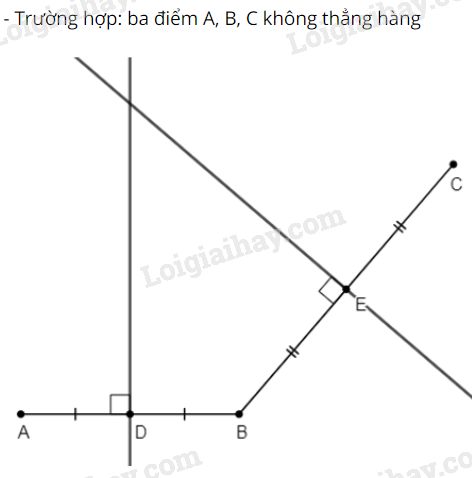
Đề bài: Vẽ đoạn thẳng ABAB dài 2cm2cm và đoạn thẳng BCBC dài 3cm3cm rồi vẽ đường trung trực của mỗi đoạn thẳng ấy.
(Vẽ hình trong hai trường hợp: ba điểm A,B,CA,B,C không thẳng hàng, ba điểm A,B,CA,B,C thẳng hàng).
- Phương pháp giải – Xem cụ thể
Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng được gọi là đường trung trực của đoạn thẳng ấy.
- Lời giải cụ thể
Sau khoảng thời gian vẽ ta được các hình sau:
Hai đường thẳng vuông góc toán lớp 7 bài 2 giải bài tập được đăng ở thể loại Giải Toán 7 và biên soạn theo phần toán hình 7 thuộc SKG Toán lớp 7. Bài giải toán lớp 7 được biên soạn bởi các thầy thầy giáo dạy giỏi toán tư vấn, nếu thấy hay hãy chia sẻ và comment để nhiều bạn khác cùng học tập.



